Impermanent Loss and Exchange Rate Level Independence in AMMs
- Neel Tiruviluamala
- Mar 22, 2022
- 9 min read
Updated: Mar 14, 2024
Introduction
Impermanent loss for automated market makers is a risk characteristic of AMMs that liquidity providers have to consider when assessing the profitability of their strategy. At a high level, impermanent loss is a measure of how much value a liquidity provider loses by exposing their assets to traders instead of simply holding them.
We recently wrote a paper where we prove that the class of geometric mean market makers (which includes Uniswap, Balancer, and others) is the simplest class of market makers to have a fundamental impermanent loss property that we call Exchange Rate Level Independence (ERLI). At a high level, this property greatly simplifies working with impermanent loss, and allows us to work in a lower dimensional space when making decisions. Geometric mean market makers turn out to be deceptively simple. If you are only familiar with AMMs like Uniswap or Balancer, you might think that all AMMs have the ERLI property. Curve’s StableSwap is a good example of an AMM whose impermanent loss characteristics are more complicated than those of G3Ms. Along these lines, carefully framing the design space (from an impermanent loss perspective) is especially important as AMMs continue to grow in complexity.
We prove that the class of geometric mean market makers is the simplest class of market makers to have a fundamental impermanent loss property, which we call the Exchange Rate Level Independence property. In this post, we’ll walk through what this property means and why it is important. Also, we’ll see that AMMs like Curve’s StableSwap don’t have this property. In summary, from an impermanent loss standpoint, geometric mean market makers are the simplest class of market makers, and all other market makers are inherently more complicated.
Visualizing Exchange Rates in AMMs
We will work in two dimensions in this post, but this generalizes to higher dimensions (see here for more). Let’s start with the Uniswap V2 Automated Market Maker (AMM) which is a Constant Product Market Maker. Consider the reserves curve


The x-axis represents the quantity of A coin and the y-axis the quantity of B coin. There are currently 20 A coins in the AMM and 160 B coins in the AMM. Assuming that the AMM is in its equilibrium state (arbitrageurs have aligned the internal AMM state with the external market exchange rate), how can we find the going exchange rate between A coin and B coin? For constant product market makers, there is a simple method: divide the quantity of B coins by the quantity of A coins. In our case, this gives us 160/20 = 8, and so the market values 1 A coin equivalently to 8 B coins. This approach to finding the exchange rate, however, does not work for more general constant function market makers. In general, if our reserves curve is given by y = f(x), then the exchange rate at a given x is given by

So, in our example,

and so the general method provides the same result as the constant product market maker shortcut. This can be represented geometrically using a tangent line to the curve at the point (20,160):

This slope has slope -8, and so we can tell that the exchange rate at (20, 160) is 8. Other states on this tangent line cannot be obtained by traders using the AMM. However, assuming the current exchange rate of 8, all of these states have the same overall value as the state (20, 160). For instance, if we value the (10, 240) state entirely in terms of B coin, we obtain 10*8 + 240 = 320 B coins, which is the same as the value of the (20, 160) state: 20*4 + 160 = 320 B coins. In particular, if we want to find the value of the state entirely in terms of the B coin, we can look at the y-intercept of the tangent line. Similarly, if we want to find the value of the state entirely in terms of the A coin, we can look at the x-intercept of the tangent line.
Visualizing Value Level Curves
In fact, this tangent line only corresponds to one of the value level curves. We could draw others and impose them on the previous diagram:

It is now clear why the point (20, 160) is special. Arbitrageurs will drive the state of the AMM to the point with the lowest value in the plane. In higher dimensions and with more complicated AMM level surfaces, finding this point is a Lagrange multipliers problem where the value function is a linear function and the constraint curve is the AMM level surface. We mention this in case it triggers any pleasant memories for the reader, but it is not necessary for the remainder of the post.
Visualizing Impermanent Loss
What happens if the external market exchange for rate for B:A goes from 8:1 to 32:1? The AMM state gets driven to the point (x, 3200/x) where x can be found as follows:

Alternatively, we can use the constant product shortcut and set x*32x = 3200, which yields x = 10 as well. Now, the value of our portfolio in terms of the B coin at the state (10, 320) is once again given by the y-intercept of the tangent line to the curve at (10, 320), which is 640 B coins.

Note that for constant product market makers, we can find the value of the portfolio in B coins just by multiplying the number of B coins in the state by two. This shortcut, however, will not work for general AMMs.
Now recall the idea of impermanent loss. What would the value of our portfolio have been if we had held our coins at the state (20, 160) instead of providing liquidity with them? We would be able to realize the current exchange rate of 32:1 at our old state (20, 160), leading to a y-intercept of 800. In other words, our portfolio value would have been equivalent to 800 B coins.

Impermanent loss is defined as the percentage of value lost from liquidity providing rather than holding. In this case, it is:

From the above diagram, it is easy to see that convex reserves curves always lead to impermanent loss for traders.
Defining Exchange Rate Level Independence
Let’s consider another scenario, one where the exchange rate goes from 32:1 to 128:1. The equilibrium state then goes from (10, 320) to (5, 640) and we can compute impermanent loss in a similar manner.

We see that the impermanent loss for this transition is

The takeaway here is that impermanent loss for this constant product market maker does not depend on exchange rate levels, but on exchange rate ratios. In other words, the 8, 32, and 128 did not particularly matter in the above discussion. Whenever the exchange rates get multiplied by 4, then, in the case of a constant product market maker, impermanent loss will be -20%. This is the property that we call exchange rate level independence.
Which Market Makers Exhibit ERLI?
Constant product market makers exhibit impermanent loss, and so do a slightly more general class of automated market makers called geometric mean market makers (G3Ms) that have the form

In our paper, we define what it means for an AMM to be exchange rate level independent (ERLI) in higher dimensions and we prove that G3Ms (up to reindexing level surfaces) are the only constant function market makers that exhibit ERLI.
Next, we’ll give a sense for why geometric mean market makers exhibit ERLI in two dimensions. It’s a harder task to show that these are essentially the only constant function market makers to exhibit ERLI, so we’ll leave that to the paper. We return to the above example, namely to the reserves curve given by y = f(x) = 3200/x.
First, let’s plot the graph using two different windows:



and then rescale the graphs so that they fit in the same sized region. In other words, think about two copies of the same graph being printed on two pieces of stretchy paper. Snip out two different pieces of the graph from the two copies and then stretch them so that they fit within the same picture frame. The above diagram illustrates this process. What’s striking about this is that the curve looks exactly the same in both frames.
This is not a coincidence. For constant product market makers, if we are given a window

and a constant j (in the above case, j was ½), then the window

will yield the exact same curve shape when the two windows are rescaled to be the same size. This explains why constant product market makers exhibit ERLI because:
a) Each state in the first window can be associated with a state in the second window by using the natural mapping.
b) The exchange rate for a state in the second window is a constant C multiplied by the exchange rate for the corresponding state in the first window. To be precise,

In the above example, since j = ½, we have that C = 4.
c) The impermanent loss for a pair of states in the first window is the same as the impermanent loss for a pair of states in the second window. This is clear since the relative heights of y-intercepts in both windows is the same.
Since the C in b) can be arbitrarily chosen through an appropriate window scaling, it follows that impermanent loss is ERLI.
The above argument can be generalized for reserves curves of the form

For these types of curves (which are level curves of G3Ms), if we are given a window

and a constant j, then the window

will yield the exact same curve shape when the two windows are rescaled to be the same size. The fact that two dimensional G3Ms satisfy the ERLI property follows analogously. All of this stems from a mathematical property known as homogeneity which we have attempted to capture pictorially above. Note that in our paper, we use a different argument than the one presented above to clean up and generalize this direction of the proof to higher dimensions.
Implications for Other Market Makers
What happens for AMMs that are not G3Ms? An interesting example is the Curve StableSwap AMM. We will focus on one level curve given by

Solving for y yields

Let’s take a look at this curve in two different windows and rescale so that the windows are the same size:
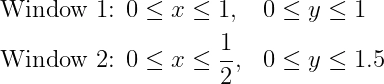


When we overlap these two curves, we notice that there is a crossing:

We did not think too much about choosing a “good” y-scaling, so you might be wondering whether there could be a better choice. However, the above crossing shows that it is impossible for there to be a y-scale for the second window such that the curves exactly overlap. Indeed, any change to the y-scale will make it so that there is no longer a curve intersection at the x position of the original crossing.
At a high level, the Curve V2 update involves rescaling windows and then shifting from an orange curve to a blue curve when a price update occurs. We can make this precise in another post if people are interested. It is a clever model that allows Curve to shift the price range in which liquidity is concentrated in a way that leverages the existing V1 StableSwap algorithm. We believe that this mechanism also shifts Curve V2’s impermanent loss profile to one that is closer to ERLI, and we might quantify this in future work.
Visualizing Impermanent Loss for a Three Dimensional AMM
We’ll end this post by including a nice consequence of defining the impermanent loss parameters correctly. We will focus on the three dimensional constant product market maker. The constraint surface is shown below. Let x, y, and z be the number of A, B, and C tokens in its reserves, and assume that traders are allowed to move the reserves subject to the constraint:


In this example, let’s assume that initially, there are 20 A tokens, 10 B tokens, and 5 C tokens in the AMM reserves. Let’s further assume that the AMM is in its stable state. That is, the tokens are valued in the external market as follows: token C is twice as valuable as token B which is twice as valuable as token A. So, they are valued according to the ratios: 4:2:1.
Then, based on a change in market conditions, an arbitrageur pulls out 3 C tokens, deposits 5 A tokens, and deposits 10 B tokens:

This is now the new stable state, meaning that the tokens in the external market are now valued according to the ratios: 25:20:2. Since the impermanent loss of a three dimensional constant product market maker exhibits ERLI, we can calculate impermanent loss with only two parameters:

According to one of the formulas derived in our paper, the impermanent loss is:

Note that this expression involves the geometric mean of t₁, t₂, and 1 divided by the arithmetic mean of the same three terms. This concept generalizes to higher dimensions and you can check out our paper for more details if you’re interested. For this particular t₁, t₂ pair, we obtain IL ~ -17.81 %. Because the impermanent loss can be written as a function of only two parameters, we can visualize it as a 3D surface. The surface is shown below.

Conclusion
In this post, we gave a high level overview of some of the key results in our recent work. In particular, we defined a property of impermanent loss that only some AMMs have: Exchange Rate Level Independence. We also built an intuition for this concept from the ground up, and explained how it can help to organize the design space of AMMs. When designing AMMs, it’s worth considering how complex the LP’s risk profile might be.
In a decentralized setting, complicated mechanisms can be difficult for users to track and parse when trying to quantify their risk. As such, it is at a minimum worth understanding the simplicity that is lost in pursuit of various performance gains. G3Ms exhibit the simplest to model risk measure and it’s unclear to us what the tradeoffs are between the complexity of the IL profile of those vs say, Curve v2 where the StableSwap reserves curve is being dynamically chosen. In future work, we will continue to investigate more complicated AMM designs, including those with dynamic updates based on internal and external price oracles.


